Bisection Method for Approximation

July 01, 2023

Bisection Method for Numerical Approximation.

As we are well aware of the fact, that if we have a function say f, the process of root finding is essentially finding a value of x such that, \(f(x) = 0\)

If the function equals to zero, then we say x is the root of a function. This method is based on the intermediate value theorem or also known as IVT for continuous function.

Let f be a continuous function on a closed interval [a, b]. Assume that m is a number between f(c) and f(b). Then $\exists$ atleast one number c in the interval [a, b], such that, \(f(a) = m\)

One can observe that we do not need a derivative of a function to compute a bisection method. The idea is halving the interval till we find the root value of the function.

Code

import numpy as np
import sympy as smp
import matplotlib.pyplot as plt
from sympy import *
from math import *

func =  lambda x : x**2 -2

a = 1
b = 3

if func(a)*func(b) > 0:
    print("Could not find the root.")
else: 
    while ((b - a)/2) > 0.00001:
        m = (b + a)/2
        if func(m) == 0:
            print(m)
        elif func(a)*func(m) < 0:
            b = m
        else:
            a = m

print(m)

xvals = np.linspace(-2, 6, num=100)
yvals = func(xvals)
plt.plot(xvals,yvals, label = "y = x^2 - 2")
plt.plot(m, func(m), "o", label = m)
plt.title("Bisection Method for Numerical Approximation")
plt.legend()
plt.show()

Output

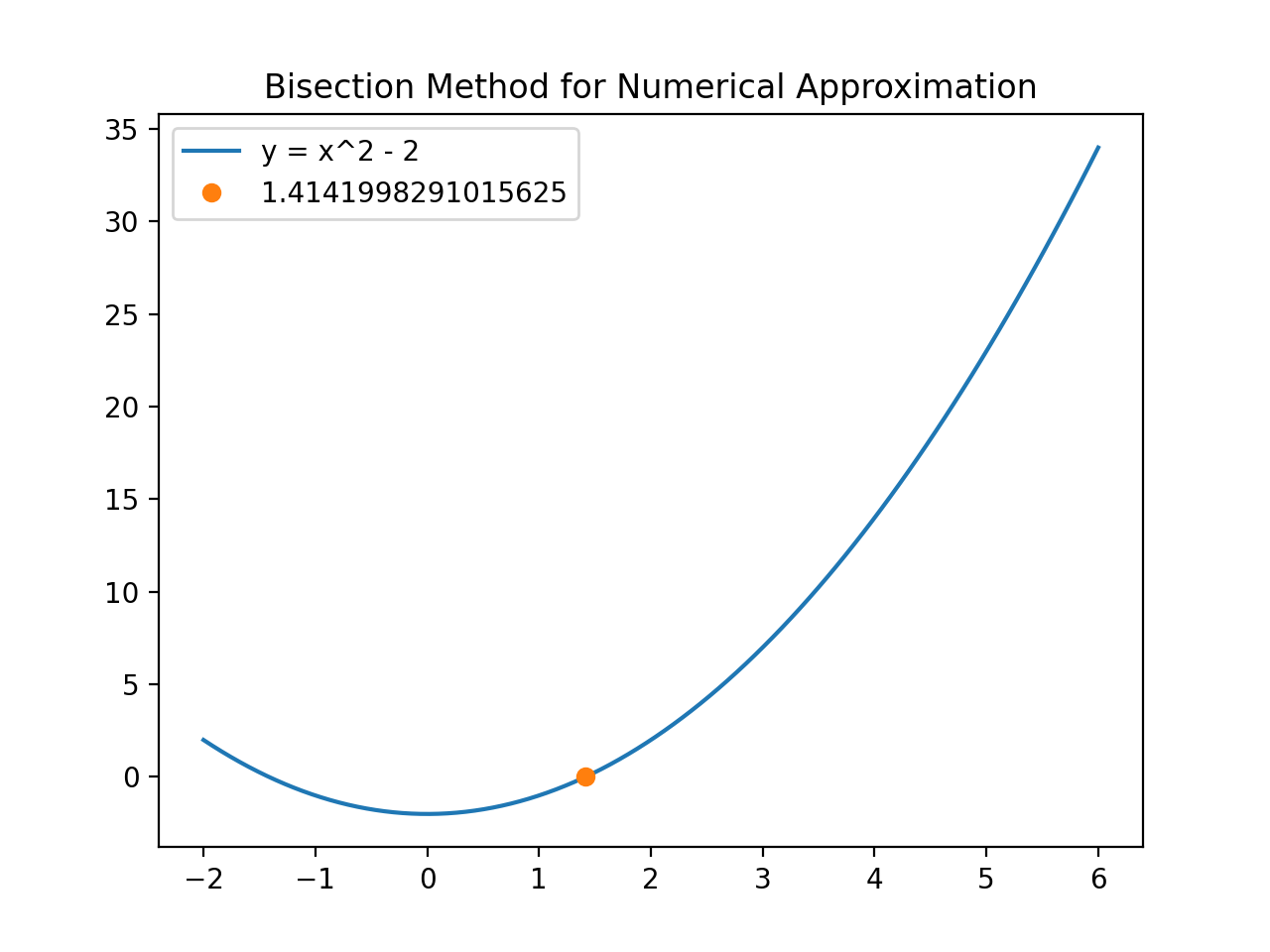
Hope this was helpful.