Newton’s method for numerical approximation.
Newton’s method is a technique used for solving an equation which is expressed in the form of real valued function, which may not have a closed form of a solution. In order for us to use the Newton’s method we need to keep in mind two things, first is that we need to know the derivative of the function and secondly we need to know is the initial guess.
Derivation.
Let us consider a function,
\(y = f(x) .......................... (1)\)
We can use the expansion formula, to be precise, Taylor’s expansion in order to expand the function in the form of,
\[f(x) = f(x_{1}) + f'(x_1) (x - x_{1}) + \frac{1}{2} f''(x_{1})(x - x_{1})^2 + ...\]
We can negelect the third term as it will be very small and we can denote it by,
\[\frac{1}{2} f''(x_{1})(x - x_{1})^2 + ... = \zeta\]
So, our expansion looks like,
\[f(x) = f(x_{1}) + f'(x_1) (x - x_{1}) + \zeta ............ (2)\]
Implies that, after substituting (2) in (1), we get,
\[y = f(x_{1}) + f'(x_1) (x - x_{1}) + \zeta\]
\[f'(x_1) (x - x_{1}) + \zeta = y - f(x_{1})\]
\[(x - x_{1}) = \frac{y - f(x_{1}) - \zeta}{f'(x_1)}\]
\[x = \frac{y - f(x_{1}) - \zeta }{f'(x_1)} + x_{1}\]
We can rewrite the equation as follows if we neglect error term being relatively small,
\[x = x_{1} - \frac{f(x_{1}) - y}{f'(x_1)}\]
\[\hspace{12 cm}\blacksquare\]
This is how we derive the newtons method.
Code
import numpy as np
import sympy as smp
import matplotlib.pyplot as plt
from sympy import *
from math import *
func = lambda x : x**2 -2
funcprime = lambda x: 2*x
#initial Guess
x0 = 2
iteration = 20
x1 = x0
guess = []
for i in range(1,iteration):
x1 = x1 - (func(x1)/funcprime(x1))
guess = [guess, x1]
print(guess)
print(x1)
print(np.sqrt(2) - x1)
xvals = np.linspace(-2, 3, num=100)
yvals = func(xvals)
plt.plot(xvals,yvals, label = "y = x^2 - 2")
plt.plot(x1, func(x1), "o", label = x1)
plt.title("Newtons Method for Numerical Approximation")
plt.legend()
plt.show()
Ouput
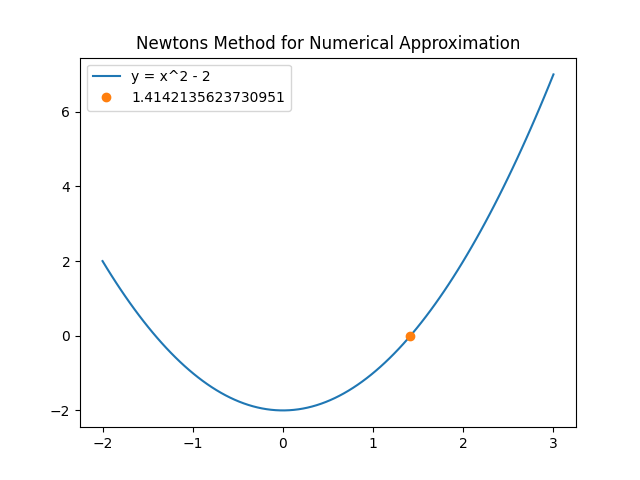
Hope you find it helpful. Thank you for reading.